Replicated Object. Part 7: Masterless Consensus Algorithm

1 Abstract

The article introduces the new generation of consensus algorithms: masterless consensus algorithm. The core part consists of less than 30 lines of C++ code. Thus it is the simplest consensus algorithm that contains several outstanding features allowing to easily developing complex fault-tolerant distributed services.

2 Introduction

There are only two hard problems in distributed systems:
2. Exactly-once delivery.
1. Guaranteed order of messages.
2. Exactly-once delivery.

Mathias Verraes.

Distributed programming is hard. The main reason that you should not rely on the common assumptions about timings, possible failures, devices reliability and operation sequences.

Distributed systems are truly asynchronous meaning that you do not have explicit a time bounds for your operations. And you cannot rely on the timer due to time drifting, time synchronization, garbage collector pauses, operating system unexpected scheduler delays and others. You cannot rely on network due to packet loss, network delays and network split. You cannot rely on hardware due to hard disk errors, CPU, memory and network device failures.

Redundancy and replication allows to tolerate numerous failures providing service availability. The only question is how to correctly replicate the data without losing consistency in the presence of asynchronous nature of the system and hardware or software failures. That task can be solved by using consensus algorithm.

3 Consensus Problem Statement

Consensus is a fundamental problem in distributed systems. It allows to provide safety guarantee in distributed services. The most common usage is to obtain an agreement on sequence of operations providing linearizable form of consistency. As a consequence, the agreement on sequence of operations provides exactly once semantics and preserves the operations ordering. Combining distributed operations sequence agreement together with state machine replication approach we can easily implement fault tolerant services with consistent shared state.

4 Overview

Let's briefly discuss existent approaches that solve distributed consensus problem.

4.1 Master-based Consensus

The first generation algorithms are the master-based consensus logic. Currently those algorithms are widespread among different services. The most popular and well-known implementations are Paxos, Zab and Raft. They have the following features in common:

1. Master makes a progress. At any time to make a progress there is a stable master (leader) which is responsible for handling all write and/or read requests.
2. Leader election. If there is no leader (e.g. leader has been crashed) the first unavoidable step is to elect the leader using so called "leader election algorithm". The system cannot make a progress unless the leader is elected.

Second point is the reason of write unavailability for a relatively large time periods (could be from seconds up to minutes) under any kind of leader failure.

Whereas Basic Paxos doesn't contain explicit leader the algorithm still is affected by the issues mentioned above. The reason is that the crash of the proposer that has received the majority of accepted votes requires appropriate handling by using specific timeout mechanism. Actually, Basic Paxos algorithm effectively performs leader election on each step. Multipaxos just optimizes that behavior by using the stable leader thus skipping prepare and promise phases.

4.2 Multimaster Consensus

The second generation consensus algorithms utilizes multimaster approach. They include quite recent implementations like EPaxos and Alvin. The common idea here is to avoid stable and dedicated master for all commands. They use temporary master for specific command instead. The approach still utilizes the idea of master but per-command basis meaning that on each incoming request from the client to replica that replica becomes a leader for the client command and performs necessary steps to commit incoming client request.

The algorithms have the following features in common:

1. Master per-command basis only. There is no stable master.
2. Utilizing fast-path quorum approach. It decreases the number of replica to be contacted thus reducing overall latency to commit the command.
3. Dependency resolver. It allows to process independent requests in parallel without any interference.
4. Leader election on failure. If the command is not committed a new elected leader for that specific command is responsible for commit it. This item obviously includes the leader election step to be performed.

The second generation algorithms have significant advantages over the first generation algorithms because they reduce the latency needed to agree and commit the commands for a price of the overall code complexity. I would like to emphasize that currently available publications of multimaster consensus algorithms do not include detailed description and safety consideration of cluster membership changes unlike e.g. raft consensus algorithm publications.

4.3 Masterless Consensus

The final generation is the masterless consensus algorithms. They use the following ideas:

1. No master. At any time there is no any master. Any replica is indistinguishable from each other.
2. No failover. The algorithm does not have any special failover logic and automatically tolerates failures by design.

5 Masterless Algorithm

This section introduces the masterless consensus algorithm.

5.1 Problem Statement

The classical consensus problem statement requires to agree on some single value from a proposed set of values. The masterless consensus algorithm slightly modifies that requirement which makes it more practical and effective. Because the final result is having the same sequence of operations on each replica the problem statement is reformulated in the following way: obtain the agreement on the same sequence of values or messages where sequence may contain the proposed values only. Sequence of values must contain at least single element meaning that the sequence must not be empty.

Thus the requirement of having the same and the only value is transformed into the requirement of having the same sequence of operations. Effectively the sequence can be treated as the "classical" value to be agreed on.

5.2 Brief Description

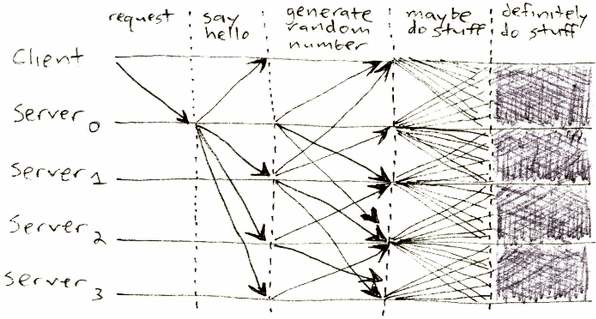
The base idea is to:

1. Send the messages by client within steps. Each replica on a single step may propose the only message. To propose next message replica must increase the current step by 1.
2. Broadcast the state to spread the knowledge about messages in progress.
3. Sort the messages deterministically.
4. Commit sequence of messages ensuring that other replicas have the same messages and there are no additional messages for the current step.

6 Naive Approach

The naive approach demonstrates the mentioned base idea. I briefly describe the model and data structures that I am going to use.

Each replica cooperates with the group of replicas by broadcasting the messages. It is very similar to actor model where each actor uses the messages to exchange the information and handle external events.

The consensus task is to agree on the sequence of client messages. Carry represents the message sent by the client and initiates the agreement processing.

6.1 Data Structures

Each client message Carry contains payload with serialized actions to be executed on commit phase. For each Carry message we should define the comparison operators:

struct Carry
{
    bool operator<(const Carry&) const;
    bool operator==(const Carry&) const;

    // executes the client operation based on payload
    void execute();

    // payload
    // ...
};

The simplest way to implement comparison operations is to add GUID and generate it on newly created client message. Carry declaration allows us to sort client messages deterministically and independently by any replica. Along with that the client message Carry can be executed to process client requests:

Carry msg;
// to commit the client message `msg` replica executes it by invoking:
msg.execute();

CarrySet contains a sorted set of messages based on overloaded comparison operators:

using CarrySet = std::set<Carry>;

NodesSet is a sorted set of replicas (nodes). Each node has unique identifier NodeId:

using NodesSet = std::set<NodeId>;

Vote describes the remote broadcast message to share the current replica knowledge:

struct Vote
{
    CarrySet carrySet;
    NodesSet nodesSet;
};

Commit message is used to commit the client message. It contains the ordered set of client messages to be executed sequentially one by one:

struct Commit
{
    CarrySet commitSet;
};

Context structure represents execution context where sourceNode is the NodeId of the sender and currentNode is the NodeId of the current replica:

struct Context
{
    NodeId sourceNode;  // sender
    NodeId currentNode; // current
};

// at any time the context can be extracted
// by using the following function:
Context& context();

Context instance is initialized per incoming message basis. Thus invocation context().currentNode allows to obtain NodeId for the current replica while context().sourceNode contains the sender NodeId.

Any data structure can be broadcasted to the others by using broadcast function:

// broadcast commit
broadcast(Commit{setToBeCommitted});

// broadcast vote
broadcast(Vote{carries_, nodes_});

Messages can be handled by appropriate services. Each service may send any number of messages and receives specific set of messages. The following example demonstrates how to catch and handle the incoming message:

// declare service to handle incoming messages
struct MyService
{
    // handles `Carry` incoming message sent by the client
    void on(const Carry& msg);

    // handles `Vote` incoming message
    void on(const Vote& vote);

    // handles `Commit` incoming message
    void on(const Commit& commit);

    // handles `Disconnect` incoming message
    void on(const Disconnect&);

    // etc
};

6.2 Messages

The algorithm consists of 4 different types of incoming messages:

1. Client message: void on(const Carry& msg)
2. Voting: void on(const Vote& vote)
3. Committing: void on(const Commit& commit)
4. Disconnection: void on(const Disconnect&)

Let's consider each message handler in detail.

6.2.1 Carry

Client sends the message Carry to be committed. Any replica accepts the client message Carry and generates appropriate Vote message:

    // accepts new incoming message from the client
    void on(const Carry& msg)
    {
        // generates initial vote message
        on(Vote{CarrySet{msg}, nodes_});
    }

Initially replica adds received carry to Vote::carrySet and uses current known set of nodes extracted from field nodes_.

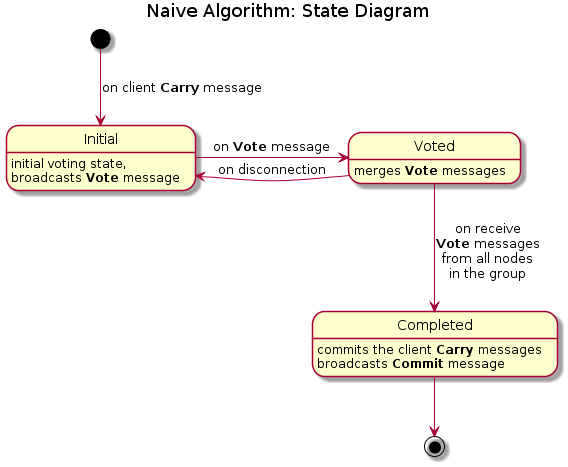
6.2.2 Vote

The main logic is placed inside the vote handler. It is the heart of the consensus algorithm. On each incoming Vote message the following sequence of operations is taken place:

1. Combining replica carries and incoming vote carries: carries_ |= vote.carrySet.
2. Checking group membership changes: if (nodes_ != vote.nodesSet). The following sequence is applied on group changing:
   • reset state to initial: state_ = State::Initial,
   • update nodes group: nodes_ &= vote.nodesSet,
   • clear votes: voted_.clear(),
3. Update current votes: add current and incoming vote.
4. If all nodes have been voted:
   • commit combined carries: on(Commit{carries_}).
5. Otherwise if state is initial:
   • change state to State::Voted,
   • broadcast updated Vote message to other replicas: broadcast(Vote{carries_, nodes_}).

6.2.3 Commit

Commit step is straightforward:

1. Change state to State::Completed.
2. Broadcast commit message to others: broadcast(commit).
3. Execute committed carries: execute(commit.commitSet).

Committed set represents the ordered sequence of client commands. Algorithm must ensure that each replica executes the same sequence of client messages.

6.2.4 Disconnect

If the node is disconnected the object receives Disconnect message. The sequence of actions to be performed is the following:

1. If disconnection takes place before client message:
   • remove the disconnected node from the group: nodes_.erase(context().sourceNode).
2. Otherwise replica:
   • generates new Vote message with updated replica group that excludes disconnected node: Vote{carries_, nodes_ - context().sourceNode} where context().sourceNode contains disconnected NodeId,
   • sends it to itself: on(Vote{...}).

6.3 State Diagram

The following diagram unites states and messages:

6.4 Code

The code below implements the naive approach:

struct ReplobSore
{
    enum struct State
    {
        Initial,
        Voted,
        Completed,
    };

    // accepts new incoming message from the client
    void on(const Carry& msg)
    {
        // generates initial vote message
        on(Vote{CarrySet{msg}, nodes_});
    }

    // main handler: accepts vote from any replica
    void on(const Vote& vote)
    {
        // committed? => skip
        if (state_ == State::Completed)
            return;
        // does not the vote belong to the group? => skip it
        if (nodes_.count(context().sourceNode) == 0)
            return;
        // combine messages from other replicas
        carries_ |= vote.carrySet;
        // check group changing
        if (nodes_ != vote.nodesSet)
        {
            // group has been changed =>
            // - remove node from the group
            // - cleanup all votes
            // - restart voting
            state_ = State::Initial;
            nodes_ &= vote.nodesSet;
            voted_.clear();
        }
        // combine votes from source and destination
        voted_ |= context().sourceNode;
        voted_ |= context().currentNode;
        voted_ &= nodes_;
        if (voted_  == nodes_)
        {
            // all replicas have been voted => commit
            on(Commit{carries_});
        }
        else if (state_ == State::Initial)
        {
            // otherwise switch to voted state
            // and broadcast current votes
            state_ = State::Voted;
            broadcast(Vote{carries_, nodes_});
        }
    }

    void on(const Commit& commit)
    {
        // committed? => skip
        if (state_ == State::Completed)
            return;
        state_ = State::Completed;
        // broadcast received commit
        broadcast(commit);
        // execute client messages combined from all replicas
        execute(commit.commitSet);
    }

    void on(const Disconnect&)
    {
        // disconnect handler
        // disconnected node are placed into Context::sourceNode
        if (carries_.empty())
        {
            // on initial stage just remove from the group
            nodes_.erase(context().sourceNode);
        }
        else
        {
            // otherwise send vote with reduced set of nodes
            on(Vote{carries_, nodes_ - context().sourceNode});
        }
    }

private:
    State state_ = State::Initial;
    NodesSet nodes_;
    NodesSet voted_;
    CarrySet carries_;
};

6.5 Examples

Let's consider different scenarios of message handling for different replicas.

6.5.1 1 Concurrent Client

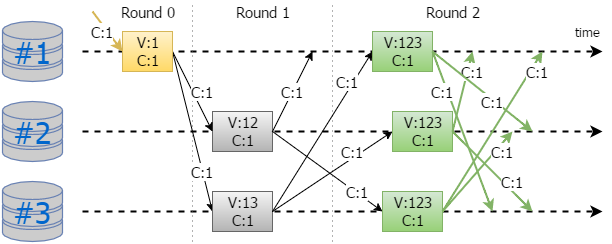
The first example demonstrates the sequence of operation in situation when the only client tries to commit the message using the group of 3 replicas:

The following designations are used:

1. There are 3 replicas: #1, #2 and #3.
2. Initial client message and corresponding state are marked using yellow color.
3. Normal voting process is marked by gray color.
4. Commit state and messages are marked using green color.
5. C:1 means carry message from the first client.
6. V:13 means that state contains votes from the 1st and 3rd replicas.
7. Round indicates the half of round trip.

It takes 2 rounds to commit the initial client message on the whole set of replicas. Thus the number of round trips is equal to 1.

6.5.2 2 Concurrent Clients

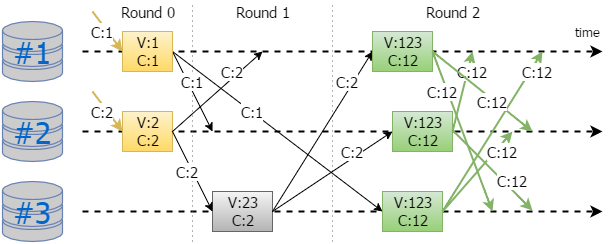
The result looks pretty similar: it takes 2 rounds to commit all client messages and the number of round trips is equal to 1 in this scenario.

6.5.3 3 Concurrent Clients

The number of round trips in that case: 0.5.

6.5.4 2 Concurrent Clients and Disconnection

The following example demonstrates the sequence of operation when the first replica is crashed:

Red color identifies the replica failure.

7 DAVE

"What are your evidences?"

Usually the consensus algorithms must be verified. Thus I have created a special application that allows to verify distributed algorithms: Distributed Asynchronous Verification Emulator or simply DAVE.

Verification is based on the following model:

1. Distributed system contains specific number of nodes.
2. Each node may have specific number of services.
3. Each service accepts specific number of messages.
4. Each service may send any number of messages to other services.
5. All messages are delivered asynchronously.
6. At each time the node may crash. Each service on the crashed node is died and the rest of the nodes receive the Disconnect message delivered asynchronously.
7. Each service has a mailbox for incoming messages. Mailbox uses FIFO queue thus the service may process the message extracted from the head of the queue.
8. Service process messages one by one.
9. On message processing service may change its internal state or/and may send any number and type of messages to any service on any node including itself.

Services lifecycle is the following:

1. Initially the message Init is arrived synchronously for each service to create and set initial state. Service may set internal state and/or send any message to any local and/or remote service.
2. The message Disconnect is used to notify about remote node failure. context().sourceNode contains node identifier for the failed node. That message is delivered asynchronously.

To simplify verification procedure and algorithm development the following approach is used: service cannot send the message to the destination service if the destination service does not contain the method to accept that message. In that case compilation error takes place generated by compiler.

The consensus verification procedure involves the following steps:

1. DAVE initializes 3 nodes and their services.
2. Client service issues initial request. Initial request contains the message to be committed. The number of client instances varies from 1 to 3 meaning that the number of simultaneous client messages to be agreed on varies from 1 to 3.
3. Client message Carry initiates Replob service starting the consensus algorithm.
4. Finally DAVE verifies the committed entries collected from all nodes:
   1. Consensus algorithm must commit all client messages in the same order on any node.
   2. Non-failed node must contain at least 1 committed message because the first node cannot fail and always sends the message to be committed.
   3. Failed node may contain any committed prefix from non-failed node including empty prefix.

DAVE scheduler uses asynchronous message delivering and tries to handle all asynchronous variants by using brute force approach. The scheduler may choose any service with nonempty mailbox and process its head message. Along with that any node except the first one may be disconnected but the only one. Thus at any time the number of available nodes may be 2 or 3.

7.1 Verification Results

The following cases should be considered and verified:

1. 1 concurrent client.
2. 2 concurrent clients.
3. 3 concurrent clients.

Those cases cover all concurrent variants for 3 replicas.

7.1.1 1 Concurrent Client

DAVE provides the following statistics for that execution:

global stats: iterations: 61036, disconnects: 54340

All verification checks were passed.

7.1.2 2 Concurrent Clients

DAVE provides the following outputs:

Verification failed: firstCommitted == nodeCommitted, must be agreement among the same
  sequence of messages, node #0: {:112565}, node #2: {:112565, :112566}
Failed sequence: {0, 0, 2, 2, 2, 0, 0, 0, 0, 0}
invoking: Apply 0=>0 [trigger]
invoking: Apply 1=>1 [trigger]
invoking: Vote 0=>2 [trigger]
invoking: Vote 1=>2 [trigger]
invoking: node disconnection: 1 [disconnect]
invoking: Vote 1=>0 [trigger]
invoking: Vote 2=>0 [trigger]
invoking: Commit 2=>0 [trigger]
invoking: Vote 0=>2 [trigger]
invoking: Commit 0=>2 [trigger]
Max fails reached
global stats: iterations: 56283, disconnects: 50002

"Cocainum"

Non-failed nodes #0 and #2 have different commit sequence because node #2 has additional committed message with id=112566. Let's consider the output message sequence in detail:

N:13 means that nodes_ variable contains #1 and #3 replicas while N:123 contains the whole set of nodes. Red color designates the replica failure event and corresponding messages. D:2 identifies the propagation of failure of #2 to corresponding node.

This diagram depicts that #1 and #3 nodes have different committed sequences: C:1 and C:12 respectively. The reason is that the first replica has been changed the nodes_ set and commit the sequence without waiting for the message from the failed node. Due to differences in a valid set of replicas N:13 for #1 and N:123 for #3 the committed sequences C:1 and C:12 accordingly differ from each other.

7.1.3 3 Concurrent Clients

In this case DAVE found the following sequence:

Verification failed: firstCommitted == nodeCommitted, must be agreement among the same
  sequence of messages, node #0: {:304, :305, :306}, node #2: {:304, :306}
Failed sequence: {0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0}
invoking: Apply 0=>0 [trigger]
invoking: Apply 1=>1 [trigger]
invoking: Vote 1=>0 [trigger]
invoking: Vote 0=>1 [trigger]
invoking: Apply 2=>2 [trigger]
invoking: Vote 2=>0 [trigger]
invoking: Vote 2=>1 [trigger]
invoking: Commit 1=>0 [trigger]
invoking: Commit 0=>1 [trigger]
invoking: node disconnection: 1 [disconnect]
invoking: Vote 2=>0 [trigger]
invoking: Vote 0=>2 [trigger]
invoking: Commit 2=>0 [trigger]
invoking: Vote 1=>2 [trigger]
invoking: Commit 0=>2 [trigger]
invoking: Commit 1=>2 [trigger]
Max fails reached
global stats: iterations: 102, disconnects: 91

Again, non-failed nodes #0 and #2 have unequal committed sequence. The following picture represents the sequence of operations:

The same reason causes the same consequences: differences in nodes group causes inconsistent committed sequences.

8 Calm Masterless Consensus Algorithm

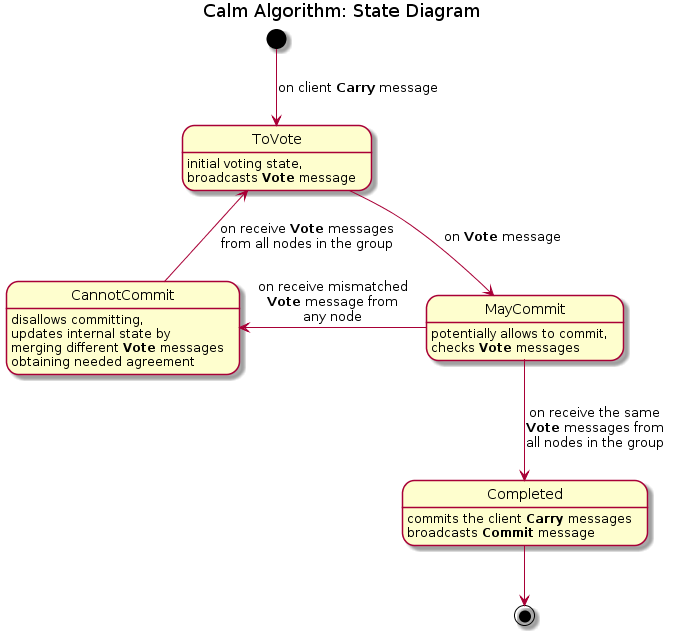
Calm algorithm resolves the found issues. The main differences are:

1. The logic splits Voted state into MayCommit and CannotCommit states.
2. MayCommit allows to commit the set of client messages CarrySet once the replica receives the same Vote messages from all alive replicas.
3. Otherwise the replica switches the state to CannotCommit and retries the voting process.

8.1 State Diagram

The following diagram represents the logic described above:

8.2 Code

The code below represent the final verified version of the "calm" algorithm:

struct ReplobCalm
{
    enum struct State
    {
        ToVote,
        MayCommit,
        CannotCommit,
        Completed,
    };

    // the following methods utilize the same logic as before
    void on(const Carry& msg);
    void on(const Commit& commit);
    void on(const Disconnect&);

    // the heart of the verified "calm" algorithm
    void on(const Vote& vote)
    {
        // committed? => skip
        if (state_ == State::Completed)
            return;
        // does not the vote belong to the group? => skip it
        if (nodes_.count(context().sourceNode) == 0)
            return;
        if (state_ == State::MayCommit && carries_ != vote.carrySet)
        {
            // if there is changes in client messages =>
            // we cannot commit and need to restart the procedure
            state_ = State::CannotCommit;
        }
        // combine messages from other replicas
        carries_ |= vote.carrySet;
        // combine votes from source and destination
        voted_ |= context().sourceNode;
        voted_ |= context().currentNode;
        if (nodes_ != vote.nodesSet)
        {
            // group has been changed =>
            // remove node from the group
            if (state_ == State::MayCommit)
            {
                // we cannot commit at this step if the group has been changed
                state_ = State::CannotCommit;
            }
            nodes_ &= vote.nodesSet;
            voted_ &= vote.nodesSet;
        }
        if (voted_ == nodes_)
        {
            // received replies from all available replicas
            if (state_ == State::MayCommit)
            {
                // may commit? => commit!
                on(Commit{carries_});
                return;
            }
            else
            {
                // otherwise restart the logic
                state_ = State::ToVote;
            }
        }
        if (state_ == State::ToVote)
        {
            // initially we broadcast our internal state
            state_ = State::MayCommit;
            broadcast(Vote{carries_, nodes_});
        }
    }

private:
    State state_ = State::ToVote;
    NodesSet nodes_;
    NodesSet voted_;
    CarrySet carries_;
};

The main difference is the following. On any nodes_ or carries_ changing the algorithm forbids going to the commit stage and restarts the voting process from the beginning.

8.3 Examples

8.3.1 1 Concurrent Client

This diagram is similar to the previous algorithm diagram.

Characteristics:

• Round trips: 1
• Messages:
  • Client: 1
  • Vote: 6 (6 per single client message)
  • Commit: 6 (6 per single client message)

8.3.2 2 Concurrent Clients

The main difference is the increased number of round trips from 1 to 1.5 required to commit the sequence. The reason is that each replica has to go through the state V:123 C:12 with State::CannotCommit before committing to ensure consistency and correct propagation the state across all replicas.

Characteristics:

• Round trips: 1.5
• Messages:
  • Client: 2
  • Vote: 12 (6 per single client message)
  • Commit: 6 (3 per single client message)

8.3.3 3 Concurrent Clients

Case seems to be the same: the number of round trips is increased on 0.5 from 0.5 to 1 with the same reason: each replica has to go through the state V:123 C:123 with State::CannotCommit.

Characteristics:

• Round trips: 1
• Messages:
  • Client: 3
  • Vote: 12 (4 per single client message)
  • Commit: 6 (2 per single client message)

8.4 Overall Characteristics

The table below represents characteristics and number of different messages under typical conditions:

Concurrent Client Messages	Round Trips	Total Votes	Total Commits	Votes per Client	Commits per Client	Total Messages per Client
1	1	6	6	6	6	12
2	1.5	12	6	6	3	9
3	1	12	6	4	2	6

Algorithm demonstrates nonobvious feature: increasing concurrency decreases the number of messages required to commit the client messages.

8.5 Calm Verification Results

DAVE executions showed that all test were passed successfully. The table below represents the collected statistics based on different DAVE running:

Concurrent Messages	Set of Nodes Accepted Client Messages	Total Verified Variants
1	#0	59 986
2	#0, #1	148 995 211
3	#0, #1, #2	734 368 600

9 Discussion

Masterless approach, by definition, means that at any time there is no master. Thus any node is responsible to propagate the client request to the replica group. It is achieved by broadcasting the state to the destination nodes. Thus the algorithm eliminates failover part completely which is crucial and one of the most complex part for other generations of consensus algorithms.

As a consequence client may send request to any node. Thus the algorithm is ready for geo-distributed datacenter replication because the client may choose the closest node that belongs to the same datacenter. The required number of round trips to synchronize and agree on the same sequence is equal to 1 approximately in most common cases. It makes suitable for the wide range of applications including distributed storages, persistent queues, real-time data analysis and on-line data processing.

Additionally, the broadcast design allows to tolerate with a variety of network failures providing robust data exchanging model. Periodic connectivity issues do not affect the replicas and commit may be easily propagated to be accepted by each node.

Finally, the algorithm contains smooth replicas degradation meaning that the group may dynamically shrink due to node failures or different network issues. E.g. algorithm is capable to preserve safety under network split. The whole spectrum of failures and appropriate algorithm changing will be considered in subsequent article.

10 Conclusion

Masterless approach is the completely new generation of the consensus algorithms. Along with that it is the simplest known consensus algorithm. The algorithm reduces the number of node roles and makes replicas indistinguishable allowing logic unification. That unification significantly reduces the algorithm complexity providing straightforward symmetric implementation based on the message broadcast to each replica within the group. Moreover, the masterless algorithm partially includes group membership changes providing smooth set of replicas degradation.

The described "calm" masterless algorithm is not the only approach. There are various set of algorithms that have different and distinct features. Stay tuned!

References

[1] Article: The Consensus Problem in Unreliable Distributed Systems (A Brief Survey), Michael J. Fischer.

[2] Article: Linearizability: A Correctness Condition for Concurrent Objects, Maurice P. Herlihy etc.

[3] Wikipedia: State machine replication.

[4] Article: Paxos Made Simple, Leslie Lamport.

[5] Article: A simple totally ordered broadcast protocol, Benjamin Reed etc.

[6] Article: In Search of an Understandable Consensus Algorithm (Extended Version), Diego Ongaro.

[7] Article: There Is More Consensus in Egalitarian Parliaments, Iulian Moraru etc.

[8] Article: Be General and Don’t Give Up Consistency in Geo-Replicated Transactional Systems, Alexandru Turcu etc.

[9] Documentation: The Raft Consensus Algorithm.

[10] Github: Distributed Asynchronous Verification Emulator aka DAVE.